“As ye randomise, so shall ye analyse”.
Stephen Senn, 2004.

Abstract

Assessing the effects of a treatment involves comparing it with no treatment or an alternative treatment. Although there are scattered examples of formal treatment comparisons during the 18th and 19th centuries, it was not until the 20th century that methods for researching treatment comparisons began to be developed in earnest. During the first half of the century, clinical and public health researchers used alternation to generate unbiased treatment comparison groups of people receiving different treatments. During the second half of the 20th century, concealed random allocation of participants gradually replaced alternate allocation. The unbiased treatment comparison groups created in this way initially differed only by chance. However, these initially unbiased comparison groups began to become biased as a result of biased loss of research participants and other differences. Researchers recognised during the 1950s that protection against the biases resulting from non-random losses from initially randomized groups could be addressed by applying an ‘intent(ion)-to-treat (ITT) principle’ in designing and analysing randomised trials. Although support for this principle has not been unanimous it has become widely accepted, including by drug licensing authorities. The key current challenge is for authors of trial reports to be more transparent about the measures they have taken to implement ‘the intention-to-treat principle’ in their pursuit of unbiased treatment comparisons.

Assembling fair treatment comparison groups

Good and bad effects of treatments are sometimes so dramatic that they can be recognised reliably using informal before-and-after treatment comparisons. Relief of pain after spinal injection of a powerful analgesic, or allergic reactions to drugs, are examples. Much more usually, important wanted and unwanted effects of treatments are not dramatic and cannot be reliably detected using informal comparisons. In this common situation, detecting real treatment effects entails comparing sufficiently numerous people who have received one of two or more alternative treatments, or by comparing contemporaneously those who have received a treatment with those who have not.

If the results of treatment comparisons are to be trustworthy, the comparisons need to be fair. In particular, the people in the different treatment comparison groups need to be alike (differing only by the play of chance), not only in respect of factors known to influence treatment outcomes (chronic illness, for example), but also in other, undocumented ways (genetic predisposition, for example), some of which may not even have been conceptualised.

Ways of creating fair treatment comparison groups began to be applied during the 19th century (Chalmers et al. 2011 ), and explicit consideration of the methodological principles entailed began to appear during the first half of the 20^th century (Sinton 1926; Martini 1932; Hill 1937; Gaddum 1940; Bell 1941; Medical Research Council 1944). Initially, alternate allocation was used to assign patients to one or other of the different treatments to be compared. By the middle of the 20th century, random allocation to comparison groups had begun to be used in preference to alternate allocation (Chalmers et al. 2011). This was mainly because of concern that knowledge of upcoming allocations (whether from an allocation schedule based on alternation or on an unconcealed random allocation schedule) could lead those recruiting participants for treatment comparisons to tamper with the schedule, thus undermining its purpose (Chalmers 2010). It may also have reflected an awareness that even strict alternation could not be relied upon to generate unbiased comparison groups (Mainland 1952, p 268).

In the late 1940s, concealed random allocation was used to generate comparison groups in the British Medical Research Council’s celebrated multicentre controlled trial of streptomycin in patients with pulmonary tuberculosis (MRC 1948). In particular, the details of the allocation schedule were concealed from those entering patients into the trial (Armitage 1960 p 16). This blinding was to prevent foreknowledge of upcoming allocations, thus reducing any temptation, conscious or unconscious, to undermine strict random allocation and so risk introducing selection bias (Chalmers 2005; Chalmers et al. 2011). As one senior contributor to the early history of randomised controlled trials later observed: “Randomization was introduced to control selection biases, not for any esoteric statistical reason” (Doll 2002). Austin Bradford Hill, director of the MRC’s Statistical Research Unit, explained that “our rather elaborate technique of sealed envelopes has been developed merely to ensure that no bias creeps in during this allocation. It has no other magical virtues.” (Hill 1960 p 170)

The 1948 report of the MRC’s streptomycin trial was widely hailed as a landmark in the development of unbiased treatment comparisons. The trial provided an exemplar for further MRC controlled trials in an exceptional programme of randomized comparisons assessing a wide variety of interventions during the 1950s and 1960s (Chalmers 2013).

The key figure in these developments was the statistician Austin Bradford Hill. Hill had come to international attention since 1937 through successive editions of his popular textbook Principles of Medical Statistics (Hill 1937), and through his prominent articles about ‘The Clinical Trial’ published in the British Medical Bulletin (Hill 1951) and the New England Journal of Medicine (Hill 1952). A very relevant but less well-known contemporary publication was Elementary Medical Statistics: The Principles of Quantitative Medicine (Mainland 1952). Its author – Donald Mainland – was a British physician who had emigrated initially to Canada, and subsequently to the USA. Doug Altman has celebrated this remarkable man in a biographical article commissioned for the James Lind Library (Altman 2017).

Maintaining fair treatment comparison groups

Strict random allocation of eligible participants to one of two or more comparison groups provides a foundation for making fair (unbiased) comparisons of the effects of treatments. This random allocation means that any differences in the characteristics of the participants in the comparison groups before treatment can reasonably be assumed to reflect the play of chance. This provides the basis for inferring treatment effects if pre-specified outcomes differ between groups after treatment.

Allocation to treatment comparison groups needs to take place as late as possible before the initiation of treatment. Statistician David Newell once worked with a surgeon who took this advice so literally that he had a silver coin sterilized along with the scalpels, waited until the patient’s abdomen had been opened and the diagnosis confirmed before he tossed the coin right there in the operating theatre to decide to which comparison group each patient would be allocated (Newell 1992)!

Random allocation of trial participants to treatment comparison groups abolishes allocation (selection) bias if there is no differential exclusion or loss of participants from the groups (randomized cohorts) as they had been initially constituted. The longer the trial lasts, however, the greater the likelihood that such losses will occur and that they will compromise the unbiased balance achieved using random allocation.

Some of the reasons for biased loss of participants cannot be avoided (death, for example). Other sources of bias could and should be avoided (for example, by strenuous efforts to track down and include missing outcome data, even for participants who have decided to withdraw from further treatment or trial visits).

The Figure below uses a randomized comparison of medical and surgical treatments in which some very ill patients randomized to surgery died before their surgery could be organised. Should these patients be excluded from analysis? As shown in the Figure, doing that would result in an unfair bias against those allocated medical treatment from which similar very ill patients had not been excluded. To avoid bias, the challenge is to try to preserve the initial comparability of groups created using random allocation – application of a design and analysis strategy that came to be designated ‘the intention-to-treat principle’ (see Hill 1961).

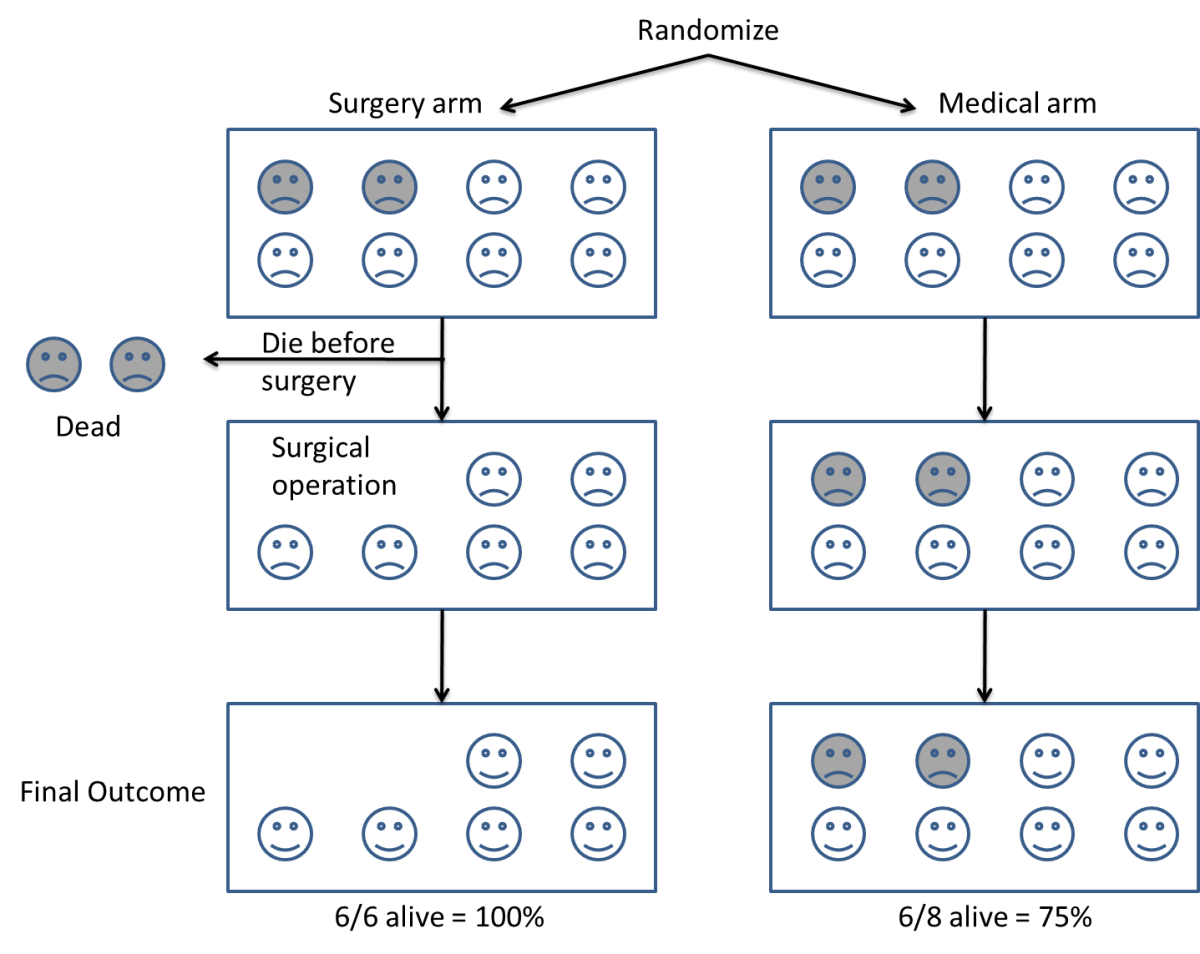
Figure: If some patients are excluded from the final analysis, such as the two very ill patients who did not survive long enough to have the surgery to which they had been assigned, subsequently observed differences in characteristics may reflect the patients analysed, not differences in the treatments allocated to them (from Evans et al. 2011 www.testingtreatments.org).

Click here for a cartoon explanation of ‘the intention-to-treat principle’:

An early application of the principle was presented by Joseph Bell in his report of a controlled trial of whooping cough vaccine initiated in 1936 in Virginia, USA, with professional support from the Norfolk City Union of King’s Daughters Visiting Nurse Association. Bell provides us with an early and remarkable example of the measures he took to establish and maintain fair treatment comparisons (Bell 1941). This entailed including all individuals allocated to one or other of the two comparison groups, whether or not they actually received the treatment assigned to them. This was an early example of what came to be recognised by others during the 1950s and which was designated twenty years later by Hill (1961) as ‘the intention-to-treat principle’.

Furberg (2009) and Chalmers (2010a) have drawn attention to Bell’s detailed account of the steps he took to maintain a fair comparison between children allocated to pertussis vaccine and those allocated to a control group. Here is an excerpt from Bell’s account (Bell 1941 pp 1536-37):

“The first problem was that of locating for observation a group of children to be vaccinated, identical, in all attributes, which might influence the occurrence and recognition of pertussis, with another group to receive no vaccine. It is impossible to select such identical groups because many of the attributes involved are not known, and many of those that are known cannot be quantitatively assessed; and, furthermore, even if such attributes could be made identical in the two groups at any one moment, they would not remain identical throughout the time necessary for adequate observation. Some attributes without apparent influence on the results may under certain circumstances be of real importance.

The only practical approach appeared to rest in the selection of two groups, each of which is a random sample of the combined groups in the exact sense of the term. Thus only can the prediction be made that should the vaccine have no real influence on the occurrence of pertussis, the occurrence in each group will approximate that of the combined group, deviating therefrom strictly within the range of chance sampling variation. On the other hand, if the vaccine confers real protection against the disease, or otherwise really influences its occurrence, the occurrence in each group will differ from that of the combined group outside the range of chance sampling variation. Obviously it is not practically possible to preselect two large strictly random groups of children who are representative of the general population and to ensure that every child in one group receives the vaccine while every child in the other group receives no vaccine during the observation period. Children in the general population have the prerogative to refuse vaccine offered and the liberty to obtain other vaccine when desired. In these premises there is no known way of changing the two groups so that one would include only children actually vaccinated, and the other include only children not vaccinated, without destroying the randomness of the selection and to that extent possibly invalidating the answer to the question asked. After it has been established that the vaccine confers protection, then questions concerning the amount and duration of such protection might in part demand direct comparison of the experience of the children actually vaccinated with those not vaccinated, providing adequate data are at hand to equalize the two groups with respect to attributes which apparently influence the occurrence of the disease.

For this report, the approach to the primary problem involved the preselection of two large strictly random groups of children and the subsequent injection of a large proportion of only one group with the vaccine. All analyses herein presented are a comparison of the experience of such preselected groups regardless of their actual status with respect to receiving the vaccine. The difficulties encountered in this approach are chronologically described in detail so that the reader may evaluate any possible errors involved,” (Bell 1941 pp 1536-37)

The methodological principle – trial planning and analysis by treatment allocated, but not necessarily received – applied by Joseph Bell may have been applied in other contemporary clinical trials, but it seems that its first mention as a methodological principle in a textbook may have been in 1952, in the first edition of Elementary Medical Statistics authored by clinical epidemiologist Donald Mainland. In a section of the book entitled ‘On Planning a Simple Experiment’, a subsection entitled ‘Intercurrent events’ addressed the problem resulting from unforeseen events that may occur during any treatment. This may happen after random allocation and be known or suspected to influence the outcome of a clinical trial. Mainland listed five events to illustrate the challenge (Mainland 1952a, p 109):

1. The treatment under test may have to be supplemented for the good of the patient. In the investigation of the streptomycin treatment of tuberculosis some patients had to receive lung collapse treatment by the introduction of air into the pleural or peritoneal cavity.
2. Complete change of treatment may be necessary in one or more patients.
3. A patient may incur an accident or disease, which may be (a) obviously associated with the original disease or with the treatment under test, (b) obviously not associated with either, or (c) have a possible association with them.
4. Treatment may be temporarily suspended owing to the patient’s business or domestic affairs.
5. A patient may be lost, e.g., by removal from the city, by his failure to persevere with the treatment, or by death.

“In deciding what should be done with data from any such patients the criterion must always be whether their inclusion or omission would introduce bias. Unless the appropriate decision is obvious, the best plan is to analyse all the data together, then to analyse the special cases and the main series separately. [our emphasis] An effort should be made to see if useful information can be obtained from the whole series up to the time that the special event occurred. (In the more complex methods of analysis of mensuration data there are ways of estimating the most likely values of missing items and then allowing for the defectiveness of such estimates)”  (Mainland 1952 p 109)

This topic is one of the many matters on which Donald Mainland expanded in the second edition of his textbook Elementary Medical Statistics (Mainland 1963). This included a chapter on ‘Lost information’, focusing on strategies rather than statistical procedures, and discusses how to minimise losses and how to analyse data when there are missing observations.

Publication of the first edition of Mainland’s important book (Mainland 1952; Altman 2017) coincided with the publication of two prominent articles by Hill entitled ‘The Clinical Trial’, one published in the British Medical Bulletin (Hill 1951), the other in the New England Journal of Medicine (Hill 1952). These two papers attracted a great deal of attention. Hill notes in the former that ‘The aim is to allocate the patients to the ‘treatment’ and ‘control’ groups in such a way that the two groups are initially [our emphasis added] equivalent in all respects relevant to the enquiry’. However, neither of Hill’s two articles explains how to address possibly biased departures from the comparison groups that had been generated using random allocation.

Hill’s articles and Mainland’s book ushered in what Shapiro and Shapiro (1997) have dubbed ‘an avalanche of American and British books and symposia devoted to clinical trials. Initially, this consisted of books and meetings focussing on statistical methods – for example, the 5^th (1952) and 6^th (1955) editions of Hill’s Principles of Medical Statistics, and books authored by Leon Bernstein and Miles Weatherall (1952), and Gustav Herdan (1955).

Other substantive documents focused almost entirely on preclinical research. Commenting on the report of a conference entitled Experimental Methods for the Evaluation of Drugs in Various Disease States (Whitelock et al. 1956), Harry Gold (1959) pointed out that among 21 papers covering nearly 300 pages of text there was only one report of an experiment describing an attempted controlled evaluation of drugs in human disease. Gold did not specify the report to which he was referring, but having looked through all the conference papers, it seems very likely to have been the report by Stamler and his colleagues (1956) on the effects of oestrogen in atherosclerotic disease. It was exceptional among the research work presented at the conference in having been based on coordinated participation among seven US Veterans’ Hospitals, and cooperative working with British colleagues in Edinburgh Royal Infirmary.

In the early 1950s, the wider-ranging contents of Mainland’s book contrasts with the focus in other books on statistical methodology rather than control of biases. However, in the late 1950s things began to change. In 1958, a 1-day Symposium on Clinical Trials was held at the Royal Society of Medicine in London. It was attended by 38 people, all of them British, nine of whom presented papers. The symposium was chaired by Sir Charles Dodds and supported by the drug company Pfizer. The presentations covered the Aims and ethics of clinical trials; Controls; Criteria for measurement in acute diseases; Criteria for measurement in chronic diseases; Statistical aspects of clinical trials; Clinical management; Presentation of results; and Financing of clinical trials. Importantly, the MRC statistician Ian Sutherland summarised the challenge of maintaining fair treatment comparison groups generated by random allocation (Sutherland 1958 p 53):

“In any trial, but particularly in the case of long-term treatment for a protracted disease such as tuberculosis, changes of the prescribed treatment may occur. Such changes may indicate a genuine failure of one of the treatments, perhaps due to a lack of clinical effect, or to excessive toxicity, which makes it essential for the clinician to depart from the protocol in the interests of the patient, but they may also reflect a lack of faith in one of the treatments, which may not really be justified. Substantial losses from the latter cause may disturb the similarity of the residual series of patients, and consequently bias the assessment, or even make it impossible to draw valid conclusions. The same applies to losses from observation, whether these are complete, the patient refusing to co-operate further, or partial, when necessary, observations on the progress of the patients have been missed. Both sources of bias are less potent if treatment has been blind. But the risk emphasises the general principle that, once allocated to treatment, every patient must be accounted for in the results, and changes of treatment or losses from observation kept to the unavoidable minimum.”  (Sutherland 1958 p 53).

These points were made the following year in one of sixteen chapters in Clinical Evaluation of New Drugs, for which all the contributors were American (Waife and Shapiro 1959). Two of the contributors – statisticians Louis Lasagna and Paul Meier (1959) – co-authored a chapter (pp 37-60) addressing the difficulties resulting from loss of patients from initially randomised cohorts. Thus (p 56):

“Perhaps the most common difficulty is the loss of some patients from observation. Such losses may occur for many reasons – uncooperativeness, toxicity of the drug, death, etc. This situation is generally covered in articles by a remark such as the following: ‘Seventeen patients failed to complete the course of treatment – fifteen on Regimen A and two on Regimen B. The analysis is restricted to the 113 patients who completed the treatment schedule. The analysis then presented usually takes no account of the lost patients. Now it may be that this type of analysis is the most reasonable under the circumstances, but such a study is by no means equivalent to a study that began with 113 patients and had no losses. The fact of losses introduces a new source of bias, possibly great enough to vitiate the results completely. Worse still, the experimenter may sometimes be unable to tell if his results remain valid or not. For example, if significantly more subjects are lost from the group treated with Drug A than from the group treated with Drug B, one may suspect that Drug A is in some way more objectionable than Drug B and, since more of the likely-to-be-affected group has been selected out (lost) from the group on Drug A, the remaining parts of the two groups are not strictly comparable, and no amount of statistical manipulation will make them so… There is no wholly satisfactory method for dealing with losses other than to avoid them. [our emphasis] Thus, although complete freedom from losses is often an impossible goal, it is worth great effort and expense to keep the number of losses at the absolute minimum.” (Lasagna and Meier 1959, p 56)

At about the same time, a committee of the British Pharmacological Society convened a 2-day meeting in London to address aspects of Quantitative Methods in Human Pharmacology and Therapeutics (Laurence 1959). Of the 64 people who attended, 13 (3 of whom were invited presenters) came from outside Britain (from USA, Sweden, Denmark, Netherlands and Germany). The meeting was supported by the Wellcome Trust, the Wellcome Foundation and the Ciba Foundation. Most of the contributions to the meeting were only indirectly relevant to the design and analysis of clinical trials, but one element of a presentation made by Richard Doll addressing Practical Problems of Drug Trials in Clinical Practice is relevant to the focus of the current article, that is, non-random losses from randomized cohorts (Doll 1959):

“Another point which may give rise to difficulty is what to do with the patient with whom, for one reason or another, it is impossible to complete the proposed treatment. It may be, for example, that the patient will die after the decision has been made to take him into the trial, but before the treatment has been properly begun. In this case, it is tempting to exclude him from the trial on the grounds that the trial drug has not had an opportunity to exert its effect. This is, however, quite unjustifiable as there would be no similar inclination to remove a similar patient from the control series. In general once a patient has been included in the trial, his fate must not be omitted from the results, unless it has been decided before the trial begins to exclude all patients dying within (say) the first 12 hr after the decision has been made to bring them into the trial – irrespective of which treatment they are in. A somewhat similar situation occurs if treatment has to be stopped because of side-effects. It might be argued that patients with coronary thrombosis who, in a trial of anticoagulants, could not proceed with the treatment should be excluded from the trial group. It is, however, not impossible that the factors which made them unduly susceptible to the drug would also affect the prognosis and the only proper thing to do is to stop the test drug, but to continue observations on them and retain them in the trial group. If this is not done and the number of patients withdrawn from treatment is appreciable, it becomes impossible to attach any meaning to the result of the trial. If they are retained in the trial group, the result of the trial group at least answers the question “Is any benefit obtained if I try to treat all my patients with anticoagulants?” If the patient is lost sight of in a long continued trial, the position is more difficult. The question then arises whether there is any reason to suppose that the loss of the patient is related in any way with the result of the treatment. It is seldom possible to answer this question firmly in the negative and the best thing to do is to make various postulates about the reasons why the patients have stopped attending and to see whether any of them would necessitate altering the conclusions to be drawn from the trial.” (Doll 1959, pp 218-219)

In the same year, a 328-page book entitled Medical Surveys and Clinical Trials was published (Witts 1959) and its 18 chapters cover a lot of ground. However, we have identified only one short passage relevant to our documentation of the development of thinking about application of the bias-reducing ‘intent-to-treat principle’. The passage that follows was contributed by John Knowelden (1959 p 129) and emphasizes the importance of making exhaustive efforts to achieve as complete follow-up as possible to reduce bias to the greatest extent possible:

“Sometimes the period of observation after establishing the protected and unprotected groups is relatively short, as in the trial which showed a reduction in paralytic poliomyelitis two to eight weeks after giving gamma globulin, or it may extend for years, as in B.C.G. and pertussis-vaccine trials. Whatever the duration, it is vital that the same degree of observation is paid to both groups, and this is best achieved by regular visits or follow-up examinations. This was particularly important in the Medical Research Council’s B.C.G. vaccine trial in school leavers where the control group among the negative reactors received no specific treatment. If subsequently a higher proportion of these had been lost sight of than of the vaccinated, it might have been difficult to say whether the defaulters were on average similar to the remaining controls who were observed; defaulting might have been the result of becoming infected or dying from tuberculosis, or on the other hand, because being perfectly fit, there seemed no point in returning for further examination. One of the strongest features of the B.C.G. vaccine trial was that by a combination of postal enquiries, visits by health visitors and re-examinations at mobile radiographic units 94 per cent of the 56,000 participants had been brought into contact with the teams within the first 18 months, and this proportion was virtually the same in vaccinated and unvaccinated children.” (Knowelden 1959 p 129)

Practical application of the key methodological principles emerging in meetings and in publications during the 1950s was manifested in the UK in 25 large controlled trials being reported between 1944 and 1960 (Chalmers 2013). Statistician Sheila Bird, commenting on what had been achieved, has written “The exposition of the British concept of the controlled clinical trial is astonishing for just how much had been got right within barely two decades” (Bird 2014).

Adoption of ‘the intention-to-treat (ITT) principle’ in designing and analysing controlled trials

By the late 1950s, the key role played by the MRC in the development of controlled clinical trials – and of Hill’s leadership specifically – had become widely recognised. The example which had been set by the MRC during the 1950s led the Council for International Organizations of Medical Sciences (CIOMS) to invite Hill to plan and chair a conference on ‘Controlled Clinical Trials’. The conference was convened under the joint auspices of the UN Educational, Scientific and Cultural Organisation (UNESCO) and the World Health Organization (WHO) “to discuss the principles, organization and scope of ‘controlled clinical trials’, which must be carried out if new methods or preparations used for the treatment of disease are to be accurately assessed clinically” (Bird 2014).

The conference was held over five days in Vienna between 23 and 27 March 1959 (Bird 2014). Hill had arranged for 23 papers to be presented by British statisticians, physicians and a surgeon (Hill 1960; Bird 2014). The programme of the conference in Vienna covered a wide range of issues relevant to developing expertise in the planning, conduct, analysis, and reporting of controlled clinical trials, and it attracted international interest. The organisers of the conference had not envisaged formal publication of the proceedings, but such was the demand for copies of the mimeographed papers made available to the hundred or so participants in the conference that these papers were published in a 177-page book the following year (Hill 1960).

The presentations covered ethics, criteria for diagnosis and assessment, definition and measurement, clinical trials using group comparisons, within-patient crossover comparisons, factorial designs, statistical requirements and methods, monitoring using sequential analysis, organisation of clinical trials, design of records and follow-up, and the analysis and presentation of results. The methodological presentations were brought to life with illustrative examples of trials in tuberculosis, upper respiratory tract infections, acute rheumatoid arthritis, coronary thrombosis, and cancer (Hill 1960).

The Council for International Organizations of Medical Sciences (CIOMS) also asked Daniel Schwartz, Professor of Medical Statistics at the University of Paris, to prepare a French ‘rapport interprétatif’ of the conference. Schwartz co-authored the report with Robert Flamant, Joseph Lellouch and Claude Roquette, all of whom were colleagues at the Unité de Recherches Statistiques de l’Institut National Hygiène à l’Institut Gustave-Roussy in Paris (Schwartz et al. 1960). The report opens with a 7-page introductory chapter entitled Buts et Méthodes with the following sections: Le jugement de signification; Le jugement de causalité; Constitution de groups comparables; Le tirage au sort; La suggestion du malade; L’essai anonyme; La suggestion chez le médecin; L’essai complètement anonyme; Des principes à l’application. Chapter II provides some examples of controlled clinical trials; Chapter III concerns estimation of the number of participants needed in an experiment; Chapter IV discusses the importance of defining criteria; and Chapters V and VI conclude the report by referring to additional methodological and ethical considerations.

The Vienna conference (Hill 1960; Bird 2014) was not the only gathering considering developments in testing treatments, but it may well have been the first conference in which several speakers had considered how to deal with biased losses from unbiased treatment comparison groups assembled using random allocation, and to have begun to develop a terminology for discussing the issue.

Peter Armitage, a statistician colleague of Hill’s, presented a paper on ‘The construction of comparable groups.’ Armitage asked how one should deal with non-random losses of trial participants after they had been allocated at random to comparison groups to ensure that any differences between them reflected only the play of chance. The penultimate paragraph of Armitage’s presentation reads as follows (Armitage 1960, pp 17-18):

“However carefully a trial has been planned, occasionally things will go wrong. Perhaps, after a patient has been entered into the trial, a more accurate diagnosis shows that she should have been excluded. Perhaps the wrong treatment is given, or for some reason the selected treatment cannot be given in the prescribed way. Perhaps the results of treatment have been inadequately recorded. Can these subjects be confidently excluded from the analysis? The main rule is that exclusion is safe only if one is quite certain that the mishap can apply equally easily within each treatment group. In a trial to compare the effects of radiotherapy and surgery in some form of malignant disease it might be decided to include only operable patients for whom either form of treatment could be carried out. It is likely that some of the patients allocated to the surgical group would be found, at the start of surgery, to be inoperable, but there would be less opportunity to make this discovery if the patient had been allocated to radiotherapy. Exclusion of these patients (who would be the most severely affected) would tend to favour the surgical group. For comparative purposes, therefore, they must be left in, although one would naturally wish to examine the results in the smaller group which is left when the unsuitable subjects are omitted.”

In response to the questions he had posed in the previous paragraph, Armitage enunciated the concept of analysis-by-intended-treatment (emphasis added here and subsequently) in the final paragraph of his presentation:

“If a particular treatment cannot be performed correctly on all patients to whom it was allocated, the difficulty will usually apply in any future widespread use of the treatment just as forcibly as in the clinical trial. It could, then, be argued that the complete group of patients for whom the treatment was intended gives a better indication of the effect of advocating its general use than does the smaller group for whom it was successfully applied. In the example to which I referred above, the comparison we are making is between the policy of advocating surgery, if possible, with the policy of applying radiotherapy; and this is the choice that would confront the clinician in practice.” (Armitage 1960 pp 17-18)

After Armitage’s presentation at the Vienna conference, ‘the intention-to-treat principle’ was mentioned in three other presentations. Rheumatologist Eric Bywaters described how he and his colleagues had dealt with withdrawals from randomised cohorts in trials needing longer than usual follow-up (Bywaters 1960, pp 77-78).

“In any long-term trial carried on, as we have done, over a period of years, some patients will emigrate, others will dislike their doctors and go elsewhere, some may die, others will recover and refuse treatment, still others may have their treatment changed to something else on the grounds that the evil we know is better than that we know not. How should these withdrawals be treated? The ideal is to have none, but that is only possible in a trial lasting a few hours. We have used two methods.”

1. 1. “We have tried to define carefully in advance under what circumstances a patient should be withdrawn from consideration and have confined our analysis to those still remaining in the trial and on the specified treatment at each annual point. If this is done it is essential that comparisons should be made of the starting state of each residual group at each point of time. Careful consideration must be given to the reasons for withdrawal within each treatment group. Thus an equal number in each group could be withdrawn, but drug A withdrawals could all be because having got better they failed to attend, and all drug B withdrawals could have been changed to drug A. A high completion rate should be built into the design of the trial, but this is never completely achieved.
   2. “In the second method we have analysed the group as a whole at each point in time, excluding only those who could not be assessed due to death or non-attendance, irrespective of whether they have remained on the specified therapy.

“There are objections to both these methods.” (Bywaters 1960, pp 77-78)

In a presentation on clinical trials in malignant disease, radiotherapist Ralston Paterson (1960 pp 125-133) commented as follows:

“Once admitted to the randomized group the case must not be extracted therefrom whatsoever happens and regardless of what is actually done to the patient. What in fact is being measured is the result of an intention to adopt one particular treatment policy rather than another and not the result of a treatment method carried to a conclusion. With cancer one just cannot lay down in advance any long-term treatment pattern to contrast with some other pattern and count that it can be adhered to. The initial treatment is determined by random methods, but at later stages of the proceedings the patient must be given that treatment which is then considered best.” (Paterson 1960 p 128)

Finally, the medical epidemiologist John Knowelden, also a colleague of Hill’s, drew attention to relevant aspects of the analysis of randomized trials (Knowelden 1960 pp 155-159):

“The analysis [of trial results] proper should begin with a statement of the number of patients who entered the trial and who satisfied the diagnostic criteria. An account should then be given of those patients who withdrew from the trial at different stages and the reasons for their withdrawal. Sometimes the withdrawal may be coincidental and unrelated to the treatments being given; the diagnosis may be revised and found to fall outside the category specified for the trial, an intercurrent infection or distinct additional illness may occur, or the patient may be uncooperative or be moved elsewhere. With this type of exclusion it is usually sufficient to show in the report that it occurred with equal frequency in Treated and Control groups and cannot have disturbed the group comparisons.”

 “A more difficult problem arises with exclusions which may be related to the treatments given, for example, a patient who is found to be sensitive to penicillin, who develops salicism on the agreed dosage of aspirin, or haemorrhagic complications when given anti-coagulants. There will always be a group of patients who exhibit side-effects, and while with some it may be possible to continue treatment, with others it may be necessary to stop. Exclusions of this kind operate unequally in Treated and Control groups, so that those who continue the full course are not necessarily alike as those originally allocated. Here are two alternatives:

1. The exclusions can be counted as failures to the selected treatment, and the further analysis made on a comparison between the remainder who completed Treated and Control régimes.
2. The groups, as originally allocated, can be compared in their progress, although some members failed to keep to the treatment, making here a comparison between those intended for Treated and those intended for Control régimes.

“One or other or both methods of analysis may be presented, the choice depending on whether it is important to emphasize the disadvantages of a particular therapy.” (Knowelden 1960, pp 156-7)

The ‘leitmotif’ of ‘the intention-to-treat principle’ ran through presentations to the conference made by Armitage, Bywaters, Paterson and Knowelden. This linguistically somewhat awkward designation of the measures required to protect against bias when designing and analysing randomised trials were seen as an application of ‘the Intent(ion)-To-Treat (ITT) Principle’. Subsequent methodological discussions might have been easier if alternative wording had been used to draw attention to the important distinction between trial analysis by Treatment Allocated and trial analysis by Treatment Received.

Hill did not make any reference to the Intention-To-Treat Principle in his opening and closing remarks as chair of the Vienna conference (or in any of the first six editions of his Principles of Medical Statistics. He had noted in the 6^th edition of his book that “every departure from the design of the experiment lowers its efficiency to some extent” (Hill 1955, p 245). However, the 7^th edition of Principles of Medical Statistics, published two years after the Vienna conference, was different. The chapter on clinical trials contained an important new section entitled ‘Differential Exclusions’:

“Unless the losses are very few and therefore unimportant, we may inevitably have to keep such patients in the comparison and thus measure the intention to treat in a given way rather than the actual treatment”. (Hill 1961 p 259)

This left little room for uncertainty about Hill’s view of ‘the intention-to-treat principle’ (Hill 1961, p 259). The following year, at the invitation of the Institute of Actuaries, Hill gave the Alfred Watson Memorial Lecture (Hill 1962 pp 178-191), in which he said:

“In many trials the original careful randomization of patients to treatment and control can be later disturbed by selective withdrawals of patients who cease to take a treatment or are proved sensitive to it so that they have to be withdrawn. The experiment is necessarily weakened – indeed we may on occasions have to assess the value of an intent to treat rather than a treatment”. (Hill 1962, p 184)

The term ‘intent-to-treat’ was eventually ‘canonised’ in 1977 when it was added to the index in the 10^th (Hill 1977) and subsequent editions of Principles of Medical Statistics.

Five editions of the book later, the section on ‘Differential Exclusions’ in the 12^th and final edition of the book (co-authored with Hill’s statistician son) read as follows:

“In the protocols of a proposed trial, specifications for any exclusions from it, e.g. of the old and severely ill, should be laid down explicitly in advance. They should not be determined after the entry of a patient and the allotment of a treatment. However, some exclusions at this latter point of time are usually inevitable”.

“In analysing the results of a trial we have, therefore, a vital question to consider – have any patients after admission to the treated or control group been excluded from further observation?  Such exclusions may affect the validity of the comparisons that it is sought to make; for they may differentially affect the two groups. For instance, suppose that certain patients cannot be retained on a drug – perhaps through toxic side effects. No such exclusion may occur on the placebo or other contrasting treatment, and the careful balance, originally secured by randomisation, may thereby be disturbed. Another specific example might lie in a trial of pneumonectomy versus radiation in the treatment of cancer of the lung. At operation there is no doubt that pneumonectomy would sometimes be found impossible to perform and it would seem only sensible to exclude these patients. But we must observe that no such exclusions can take place in the group treated by radiation. If we exclude such patients on the one side and inevitably retain them on the other, can we any longer be sure that we have two comparable groups differentiated only by treatment?  Unless the losses are very few and therefore unimportant, we may inevitably have to keep such patients in the comparison and thus measure the intention to treat in a given way rather than the actual treatment. On the other hand, as earlier stated, if the diagnosis of an illness needs to be confirmed by a bacteriological, or other, test, there is less objection to excluding patients who were randomly entered but in whom the test has shown the diagnosis to be wrong. The exclusions should, except for the play of chance, occur equally in the two or more groups. At the very least, though, the number of such exclusions in each group must be reported so that readers can judge whether anything has gone seriously amiss. Similarly if, after randomisation, death (or some other defined event), were to take place before treatment could be begun there should be no objection to the removal of such patients from the trial so long as the lapse of time between randomisation and the beginning of treatment is, on the average, the same in both groups. In such circumstances there is, again, no reason why the numbers should differ materially between the groups – and if they did one would need to seek an explanation. In practice the lapse of time might differ between, for instance, a group allocated to, and likely to await, surgery and a group allocated to, and immediately available for, medical treatment. Possibly the only solution here lies in the ab initio planning, e.g. that the medical case will await the treatment under trial until the corresponding surgical case enters the trial. There can be no hard and fast rules for there is no correct answer to all situations. [our emphasis] One thing that can be said is that whenever possible it would be wise to analyse the results of a trial (1) including and (2) omitting the patients that one proposes to exclude. What effect do the exclusions reveal? The question of the introduction of bias through exclusions for any reason (including lost sight of) must, therefore, always be carefully studied, not only at the end of a trial but throughout its progress. This continuous care is essential in order that we may immediately consider the nature of the exclusions and whether they must be retained in the enquiry for follow-up, measurement, etc. It will be too late to decide about that at the end of the trial.” (Hill and Hill 1991, p 226-228)

The following year (1992), in a helpfully illustrated article on the implications of ‘intention-to-treat (ITT) analysis’ for quantitative and qualitative research, David Newell (1992) used data from the Coronary Artery Bypass Surgery (CABS) trial to illustrate the consequences of failing to analyse trial results using ‘the intention-to-treat (ITT) principle’. He showed the results of an analysis of 2-year mortality rates using three methods – ‘intention-to-treat’, ‘compliers only’, and ‘as treated’ (Table).

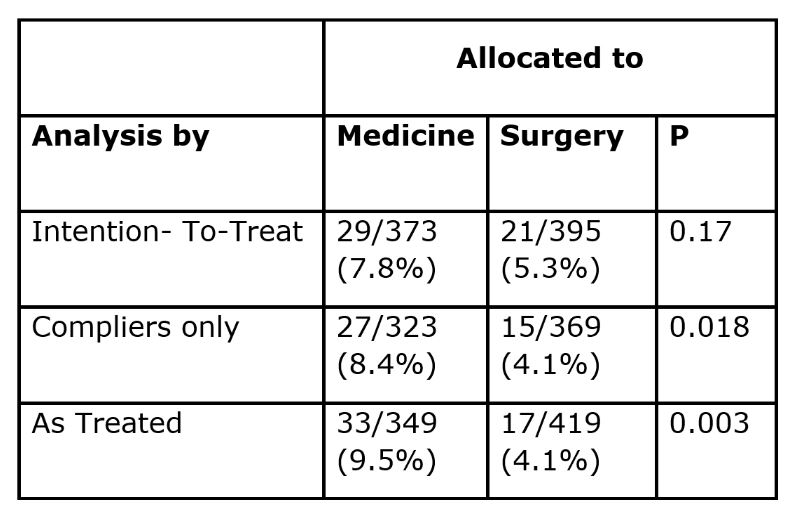
‘Intention-to-treat analysis’ (which had been used correctly by the CABS trialists) yielded a 7.8% mortality rate among patients allocated to medical treatment, and a 5.3% mortality rate in those allocated to surgery, a difference that could easily have reflected the play of chance (P=0.17). If the analysis had been restricted to those who had actually received the treatment to which they had been allocated (‘compliers’), the two mortality rates would have been statistically significantly different (P=0.018), and an analysis comparing participants ‘as treated’ would have wildly exaggerated the apparent value of surgery (P=0.003).

Adoption of ‘the intent(ion)-to-treat (ITT) principle’ in designing and analysing randomised trials

The 7^th to 12^th editions of Hill’s popular Principles of Medical Statistics published between 1961 and 1991 seem likely to have been important in promoting awareness of ‘the intention-to-treat (ITT) principle’ in the English-speaking world. This had led to widespread endorsement of the principle (see, for example, Fisher et al. 1990; Lee et al. 1991; Newell 1992; Hollis and Campbell 1999; Montori and Guyatt 2001; Fergusson et al. 2002; Wiens and Zhao 2007; Gupta 2011; White et al. 2012; McCoy 2017; International Conference on Harmonisation 1999).

However, there have been some detractors, for example, Sheiner and Rubin (1995) and Richard D Feinman. Feinman suggested that “At first hearing the idea of ITT is counter-intuitive if not completely irrational – why would you include in your data people who are not in the experiment?” (Feinman 2009).

Lack of support for the ITT principle was evident when the principle was first enunciated. No explicit reference was made to ‘the intent-to-treat principle’ (or to ‘l’intention de traiter’) in the ‘rapport interprétatif’ prepared by Schwartz and his colleagues for the Vienna conference (Schwartz et al. 1960), although their report did imply a lack of acceptance of the rationale for ‘intention-to-treat’ analysis in clinical trials requiring prolonged follow-up: “Si on prend tous les sujets au départ, sans clause d’exclusion, il se produit un grand nombre de defections, qui rend difficile ou impossible l’analyse des résultats”. Schwartz and his colleagues provide three examples of trials to highlight the issue with withdrawals, but they were not clear about how they had analysed data relating to the withdrawn patients.

There was no reference to the ITT (or to “l’intention de traiter principle”) in an article on controlled trials by Schwartz published the following year (Schwartz 1961). Furthermore, we have not been able to find any mention of the principle in L’Essai Thérapeutique chez L’Homme – either in a substantial book co-authored by Daniel Schwartz, Robert Flammant and Joseph Lellouch published ten years after the Vienna meeting (Schwartz et al. 1970), or in an English translation of L’Essai Thérapeutique chez L’Homme by the British statistician Michael Healy a decade after publication of the book.

Although ‘the intention-to-treat (ITT) principle’ is not mentioned in these books (Schwartz et al. 1960; 1970) they illustrate the problems created by withdrawals. In correspondence during the late 1990s, Daniel Schwartz made clear to Peter Armitage that he would only support the adoption of the ‘intention-to-treat approach’ if this was authorized in the trial protocol, as defining the strategy under study. In other circumstances they would regard protocol deviations as regrettable, and as a mark of unsatisfactory research methods (Armitage 1998 p 2677). Armitage commented on Schwartz’s and Lellouch’s position as follows:

“The pragmatic attitude is often taken to be exemplified par excellence by the intention-to-treat approach to the analysis of results, whereby comparisons are made between the outcomes for the complete groups assigned to different treatment regimens, irrespective of the extent of departure from the treatment schedules laid down in the protocol. Professors Schwartz and Lellouch have pointed out (in a personal communication) that this identification would go beyond their intentions. They would support the intention-to-treat approach only if this was authorized in the trial protocol, as defining the strategy under study. In other circumstances they would, I think regard protocol deviations as regrettable, and as a mark of unsatisfactory research methods”.  

“In almost any clinical trial departures from protocol are likely to occur to some extent. A patient may experience unwanted side effects; deterioration of the patient’s condition may lead the physician to prescribe alternative treatments, or the patient may decline to co-operate for any number of reasons. The trial statistician, therefore, is inevitably faced with the problem of how to take them into account in the analysis. In a trial conceived of as essentially pragmatic in nature, the investigators are likely to lean towards an intention-to-treat approach”. (Armitage 1998 p 2677-8)

Armitage goes on to list the arguments usually adduced for the ITT approach:

“The benefits of randomization are maintained; differences in outcome between the groups cannot be ascribed to systematic differences in the pre-treatment characteristics of the patients.

“The comparison is essentially one of different strategies of treatment, defined by ideal schedules but with the recognition that, in the trial just as in clinical practice, departures from these schedules will occasionally occur. In this sense, the trial may be said to simulate routine practice”.

“Any attempt to measure relative efficacy, by comparing groups of patients with 100% compliance to protocol, is deeply suspect because of selection biases”. (Armitage 1998, p 2678)

Quite apart from the differences between the Hill and Armitage position and the Schwartz and Lellouch position, surveys of clinical trials reported in major general medical journals 40 years after the Vienna meeting have shown that only half of the trial reports assessed had observed ‘the intent-to-treat (ITT) principle’ (Hollis and Campbell 1999; Ruiz-Canela et al. 2000). The surveys made clear that the phrase ‘intent-to-treat’ seemed to have different meanings for different authors; that ITT analyses were often inadequately described and inadequately applied; and that there was no consensus about how to handle deviations from randomised allocation. Despite this, trial reports that made no mention of the ITT principle were judged to have been of lower quality than those that did. In 1999, in response to this situation, the International Conference on Harmonisation published statistical principles for clinical trials. These principles emphasised that ‘primary’ analyses should be based on an application of the ITT principle.

In 2009, after considering evidence of the importance of taking account of adherence to treatment and how one should analyse and interpret clinical trials in which patients don’t take the treatments assigned to them, Curt Furberg listed the lessons learned as follows (Furberg 2009):

• “Good and poor medication adherers seem to have different prognoses.
• Good adherence to harmful drugs is associated with worse prognosis.
• Good adherence to beneficial drugs is associated with better prognosis.
• Specific reasons that could account for the relationship between good adherers and favourable outcomes and poor adherers and unfavourable outcomes remain unclear.
• There is no established method to adjust for adherence-related participant factors.
• There is no guarantee that subsets of participants with high or low adherence within two study groups are comparable in terms of risk.
• Analysis of clinical trial data by treatment administered can be misleading.
• The intention-to-treat approach to analysis remains the safest or least biased way of analysing clinical trial data.
• This is the reason why reputable medical journals and regulatory agencies adhere to the intention-to-treat approach”.

Acceptance of the desirability of ‘intention-to-treat’ analysis has prompted a series of analyses by Iosief Abraha, Alessandro Montedori and their colleagues to audit the extent to which the principal has been applied in practice by researchers. They have drawn attention to researchers’ increasing tendency to adopt the usually undefined term ‘modified intention-to-treat (mITT)’ analysis. They found that the definition of mITT was irregular and arbitrary and open to manipulation and consequently to bias (Abraha & Montedori 2010). When they compared the characteristics of trials that had reported having used a ‘modified intention-to-treat (mITT) approach’ with trials reporting having used ‘unmodified ITT’ they found that the mITT trials were significantly more likely to have made post-randomisation exclusions and were strongly associated with industry funding and authors’ conflicts of interest (Montedori et al. 2011). In a third study, Abraha and his colleagues (2015) used 43 systematic reviews of interventions and 310 randomised trials to assess whether deviation from the standard ITT analysis influenced treatment estimates of treatment effects. They found that “Trials that deviate from the ITT approach overestimate the treatment effect of meta-analyses compared with those trials that report a standard approach” (Abraha et al. 2015).

In 2019, the International Conference on Harmonisation published an addendum to its 1999 report in which it observed that the term ITT had been gradually degraded by applying it to cases where the data were missing but had been imputed (International Conference on Harmonisation 2019).

Despite the undoubted challenges and compromises entailed in applying ‘the intention-to-treat principle’ in practice, research funders, journals and readers should require trialists who state that they have used a ‘modified intention-to-treat analysis’ to state how they have handled deviations from random allocation, ineligible inclusions, and missing outcomes.

Though commonly confused, the issues of ‘deviation from allocated treatment’ and ‘missing outcomes’ are separate, and each requires its own reporting and analysis. There are several options for missing outcomes (such as ‘last observation carried forward’ and imputation in various guises), but deviations from allocated treatment, ‘the intention-to-treat principle’, remains the mainstay. In a secondary analysis it may be useful to adjust for non-adherence to allocated treatment to estimate the ‘explanatory’ effect. For example, Robert Newcombe (1988) has suggested a simple adjustment to the ITT estimate.

The conclusion reached by White, Carpenter and Horton in 2012 is worth repeating:

“Clinical trials should employ an intention-to-treat analysis strategy, comprising a design that attempts to follow up all randomised individuals, a main analysis that is valid under a stated plausible assumption about the missing data, and sensitivity analyses which include all randomised individuals to explore the impact of departures from the assumption underlying the main analysis. Following this strategy recognises the extra uncertainty arising from missing outcomes and increases the incentive for researchers to minimise the extent of missing data” (White et al. 2012).

Concluding reflections

Concealed random allocation is a key feature of fair treatment comparisons. It ensures that – at the moment of allocation – treatment comparison groups will differ only as a result of the play of chance.

From trial planning onwards, obsessional efforts are needed to protect the unbiased status of these randomised comparison groups. The longer the duration of follow-up after random allocation the more likely it will be that there will be loss of participants, missing outcome data, and non-random withdrawals, with the result that treatment comparisons will become biased.

A variety of strategies have been used in attempts to minimise and take account of biased loss of trial participants from the groups to which they have been allocated. Missing outcomes and deviation from allocated treatment are separate issues, and each requires its own reporting and analysis.

Strenuous efforts are needed to minimise missing outcomes and other important data. Greater use of record linkage to mortality registers and hospital admission statistics may help to identify missing outcomes.

Application of the intention-to-treat principle remains the mainstay for dealing with deviations from allocated treatment (Hollis and Campbell 1999). A secondary analysis may be useful to adjust an estimate of treatment effect that takes account of the extent of non-adherence to allocated treatment (Newcombe 1988).

The current lack of research transparency jeopardises the research efforts  needed to identify research design features that minimise losses when randomised cohorts are to be followed for many years. Explicit statements about post-randomisation exclusions should replace the ambiguous terminology of ‘modified intention to treat’ (Abraha and Montedori 2010).

Despite the undoubted challenges and compromises entailed in applying ‘the intention-to-treat principle’ in practice, research funders, drug licensing authorities, journal editors and readers should require trialists who state that they have used a ‘modified intention-to-treat analysis’ to make clear how they have handled ineligible inclusions, missing outcomes, and deviations from random allocation (International Conference on Harmonisation 1999; 2019). However, as observed by Austin Bradford Hill and his son David Hill more than forty years ago:

“There can be no hard and fast rules
for there is no correct answer to all situations.”
Hill and Hill, 1981

Dedication
We are indebted to the late and much missed Tony Johnson (1943-2022) and his colleague Vern Farewell for creating an invaluable annotated bibliography of early textbooks and other publications on controlled clinical trials.

Acknowledgements
In addition, we thank Sheila Bird, Diana Elbourne, Klim McPherson, David Nunan, Andy Oxman, Stephen Senn, John Simes and Steven Woloshin for providing relevant information and commenting on earlier drafts of this article.

Box: Contributions leading to recognition of the importance of applying what became known as ‘the Intention-To-Treat (ITT) principle’ in planning and analysing controlled trials. 1936 Joseph Bell. Use of ‘the intention-to-treat principle’ in a trial of pertussis vaccine 1952 Donald Mainland. Base initial analyses of clinical trials on all patients entered 1958 Ian Sutherland. Need to maintain fair comparison groups in trials 1959 Louis Lasagna & Paul Meier. Loss of patients as a major source of bias 1959 Richard Doll. Ways of dealing with the loss of trial participants 1959 John Knowelden. The need for exhaustive efforts at follow-up 1960 Austin Bradford Hill. Designed and chaired the 1959 UNESCO and WHO conference on Controlled Clinical Trials 1960 Peter Armitage. Early reference to  the concept of ‘analysis by intended treatment’ 1960 Eric Bywaters. Practical methods for follow-up to minimise losses 1960 Ralston Paterson. The need to maintain original patient allocation status 1960 John Knowelden.  The need to account for excluded randomized patients 1961 Austin Bradford Hill. Use ‘Intention-To-Treat (ITT) analyse to deal with biased exclusions 1991 Austin Bradford Hill & David Hill. The need for transparent reporting of post-allocation exclusions 1991 Lee YJ, Ellenberg JH, Hirtz DFG, Nelson KB. Is analysis of clinical trials by treatment actually received really an option? 1992 David Newell. Comparison of three methods for estimating treatment effects 1999 Sally Hollis & Fiona Campbell. Clarity needed on the meaning of ‘the intention-to-treat (ITT) principle’ 1999 International Conference on Harmonisation (ICH E9). Emphasis on ‘the Intention-To-Treat (ITT) principle’ 2010 Iosief Abraha & Alessandro Montedori. Clarity needed on the meaning(s) of ‘modified intention-to-treat’ 2019 International Conference on Harmonisation. Addendum to the Guideline on Statistical Principles for Clinical Trials on estimands and defining sensitivity analyses (ICH E9).

.

This James Lind Library article has been republished in the Journal of the Royal Society of Medicine in 2 parts.

Chalmers I, Matthews R, Glasziou P, Boutron I, Armitage P. Trial analysis by treatment allocated or by treatment received? Origins of ‘the intention-to-treat principle’ to reduce allocation bias: Part 1. JRSM 2023;116:343-350

Chalmers I, Matthews R, Glasziou P, Boutron I, Armitage P. Trial analysis by treatment allocated or by treatment received? Origins of ‘the intention-to-treat principle’ to reduce allocation bias: Part 2. JRSM 2023;116:386-394

References

Abraha I, Montedori A (2010). Modified Intention to Treat reporting in randomised controlled trials: systematic review. BMJ 340:c2697.

Abraha I, Cherubini A, Cozzolino F, De Florio R, Luchetta ML, Rimland JM, Folletti I, Marchesi M, Germani A, Orso M, Eusebi P, Montedori A (2015). Deviation from intention to treat analysis in randomised trials and treatment effect estimates: meta-epidemiological study. BMJ 2015;350:h2445. doi: https://doi.org/10.1136/bmj.h2445

Altman DG† (2017). Donald Mainland: anatomist, educator, thinker, medical statistician, trialist, rheumatologist. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/donald-mainland-anatomist-educator-thinker-medical-statistician-trialist-rheumatologist/)

Armitage P (1960). The construction of comparable groups. In: Hill AB ed. Controlled clinical trials. Oxford: Blackwell, pp 14-18.

Armitage P (1998). Attitudes in clinical trials. Statistics in Medicine 17:2675-2683. https://jameslindlibrary.org/wp-data/uploads/2023/04/Armitage-1998-Statistics-in-Medicine-Attitudes-in-clinical-trials.pdf

Bell JA (1941). Pertussis prophylaxis with two doses of alum-precipitated vaccine. Public Health Reports 56:1535—1546.

Bernstein L, Weatherall M (1952). Statistics for Medical and other Biological Students. London: E & S Livingstone.

Bird SM (2014). The 1959 meeting in Vienna on controlled clinical trials – a methodological landmark. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/the-1959-meeting-in-vienna-on-controlled-clinical-trials-a-methodological-landmark/)

Bywaters E (1960). Rheumatoid arthritis. Treatment and illustrative answers. In: Hill AB ed. Controlled Clinical Trials. Oxford: Blackwell, pp 75-83.

Chalmers I (2005). Statistical theory was not the reason that randomisation was used in the British Medical Research Council’s clinical trial of streptomycin for pulmonary tuberculosis. In: Jorland G, Opinel A, Weisz G, eds. Body counts: medical quantification in historical and sociological perspectives. Montreal: McGill-Queens University Press, 2005:309-334. https://jameslindlibrary.org/wp-data/uploads/2023/04/Charmers_2005_Statistical_theory.pdf  

Chalmers I (2010). Why the 1948 MRC trial of streptomycin used treatment allocation based on random numbers. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/why-the-1948-mrc-trial-of-streptomycin-used-treatment-allocation-based-on-random-numbers/)

Chalmers I (2010a). Joseph Asbury Bell and the birth of randomized trials. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/joseph-asbury-bell-and-the-birth-of-randomized-trials/)

Chalmers I (2013). UK Medical Research Council and multicentre clinical trials: from a damning report to international recognition. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/uk-medical-research-council-and-multicentre-clinical-trials-from-a-damning-report-to-international-recognition/)

Chalmers I, Dukan E, Podolsky SH, Davey Smith G (2011). The advent of fair treatment allocation schedules in clinical trials during the 19th and early 20th centuries. JLL Bulletin: Commentaries on the history of treatment evaluation (https://www.jameslindlibrary.org/articles/the-advent-of-fair-treatment-allocation-schedules-in-clinical-trials-during-the-19th-and-early-20th-centuries/).

Dodds C, editor (1958). Report of a Symposium on Clinical Trials held at The Royal Society of Medicine, London, 25 April.

Doll R (1959). Practical problems of drug trials in clinical practice. In: Laurence DR, ed. (1959). Quantitative Methods in Human Pharmacology and Therapeutics. London: Pergamon Press. pp 213-221.

Doll R (2002). The role of data monitoring committees,” In Duley L, Farrell B, eds., Clinical Trials. London: BMJ Books, pp 97-104.

Evans I, Thornton H, Chalmers I, Glasziou P (2011). Testing Treatments. 2nd edition. London: Pinter and Martin. p 77.

Feinman RD (2009). Intention to treat. What is the question? Nutrition & Metabolism 6:1. doi:10:1186/1743-7075-6-1

Fergusson D, Aaron SD, Guyatt G, Hébert P (2002). Post-randomization exclusions: the intention to treat principle and excluding patients from analysis. BMJ 325:652-4.

Fisher LD, Dixon DO, Herson J, Frankowski RK, Hearon MS, Peace KE (1990). Intention to Treat in Clinical Trials. In: Peace KE (ed). Statistical Issues in Drug development. New York: Marcel Dekker. pp 331-350.

Furberg CD (2009). How should one analyse and interpret clinical trials in which patients don’t take the treatments assigned to them? JLL Bulletin: Commentaries on the history of treatment evaluation. (https://www.jameslindlibrary.org/articles/how-should-one-analyse-and-interpret-clinical-trials-in-which-patients-dont-take-the-treatments-assigned-to-them/)

Gaddum JH (1940). Therapeutic trials on man. In: Gaddum JH. Pharmacology. London: Oxford University Press, pp 379-383.

Gold H (1959). Experiences in Human Pharmacology. In: Laurence DR, ed. (1959). Quantitative Methods in Human Pharmacology and Therapeutics. London: Pergamon Press. pp 40-54.

Gupta SK (2011). Intention to treat concept: a review. Perspectives in Clinical Research 2:109-112.

Herdan G (1955). Statistics of Therapeutic Trials. London: Elsevier.

Hill AB (1937). Principles of medical statistics. London: Lancet.

Hill AB (1951). The clinical trial. British Medical Bulletin 7:278-282.

Hill AB (1952). The clinical trial. New England Journal of Medicine 247:113-119.

Hill AB (1955). Principles of Medical Statistics. 6^th edition. Oxford: Blackwell Scientific Publications.

Hill AB (1960). Controlled Clinical Trials. Oxford: Blackwell Scientific Publications.

Hill AB (1961). Principles of Medical Statistics. 7^th edition. Oxford: Oxford University Press, pp 258-259.

Hill AB (1962). Alfred Watson Memorial Lecture: the statistician in medicine. Journal of the Institute of Actuaries 88:178-191.

Hill AB, Hill ID (1991). Differential exclusions. In: Bradford Hill’s Principles of Medical Statistics. 12^th edition. London: Edward Arnold. pp 226-228.

Hollis S, Campbell F (1999). What is meant by intention-to-treat analysis? Survey of published randomised controlled trials. BMJ 319:670-674.

International Conference on Harmonisation (1999). Statistical principles for clinical trials (ICH E9). Statistics in Medicine 18:1905-42.

International Conference on Harmonisation (2019). ICH E9 (R1): Addendum on estimands and defining sensitivity analyses to the Guideline on Statistical Principles for Clinical Trials (ICH E9). Statistics in Medicine 18:1905-42.

Knowelden J (1959). Prophylactic trials. In: Witts LJ ed. Medical Surveys and Clinical Trials. London: Oxford University Press. pp 118-133.

Knowelden J (1960). The analysis and presentation of results. In: Hill AB, ed. Controlled Clinical Trials. Oxford: Blackwell Scientific Publications, 155-159.

Lasagna L, Meier P (1959). Experimental Design and Statistical Problems. In: Waife SO, Shapiro AP, eds. The Clinical Evaluation of New Drugs. New York: Hoeber. pp 37-60.

Laurence DR, ed. (1959). Quantitative Methods in Human Pharmacology and Therapeutics. London: Pergamon Press.

Lee YJ, Ellenberg JH, Hirtz DFG, Nelson KB (1991. Analysis of clinical trial by treatment actually received: is it really an option? Statistics in Medicine 10:1595-1605.

Mainland D (1952). Intercurrent Events. In: Elementary Medical Statistics: the principles of quantitative medicine. London: WB Saunders Company, p 109.

Mainland D (1952). Elementary Medical Statistics: the Principles of Quantitative Medicine. Printed and bound in India. Pranava Books. 2- LB100151138852 -301 -4 sa.

Mainland D (1963). Lost Information. In: Elementary Medical Statistics: the principles of quantitative medicine. London: WB Saunders Company, pp 178-186.

Martini P (1932). Methodenlehre der Therapeutischen Untersuchung [Methodological principles for therapeutic investigations]. Berlin: Springer.

McCoy CE (2017). Understanding the intention-to-treat principle in randomized controlled trials. Western Journal of Emergency Medicine 18:1075-1078.

Medical Research Council (1944). Clinical trial of patulin in the common cold. Lancet 2:373-5.

Medical Research Council (1948). Streptomycin treatment of pulmonary tuberculosis: a Medical Research Council investigation. BMJ 2:769-782.

Montedori A, Cherubini A, Bonacini MI, Casazza G, Luchetta ML, Duca P, Cozzolino F, Abraha I (2011). Modified versus standard intention-to-treat reporting: Are there differences in methodological quality, sponsorship, and findings in randomised trials? A cross-sectional study. Trials 12:58. http://www.trialsjournal.com/content/12/1/58

Montori VM, Guyatt GH (2001). Intention-to-treat principle. CMAJ 165:1339-1341.

Newcombe RG (1988). Explanatory and pragmatic estimates of the treatment effect when deviations from allocated treatment occur, Statistics in Medicine 7:1179-86.

Newell DJ (1992). Intention-to-Treat analysis: implications for quantitative and qualitative research. International Journal of Epidemiology 21:837-841.

Paterson R (1960). Clinical trials in malignant disease. In: Hill AB (1960). Controlled Clinical Trials. Oxford: Blackwell Scientific Publications, p 125-133.

Ruiz-Canela M, Martinez-Gonzalez MA, de Irala-Estevez J (2000). Intention-to-treat analysis is related to methodological quality. BMJ 320:107-108.

Schwartz D (1961). L’expérimentation en thérapeutique. Journal de la Société Statistique de Paris 102:16-25.

Schwartz D, Flamant R, Lellouch J, Rouquette C (1960). Les essais thérapeutiques cliniques. Paris: Masson.

Schwartz D, Flamant R, Lellouch J (1970). L’essai thérapeutique chez l’homme. Paris: Flammarion.

Senn S (2004). Added Values. Controversies concerning randomization and additivity in clinical trials. Statistics in Medicine 23; 3729-3753.

Shapiro AK, Shapiro E (1997). The Powerful Placebo: from Ancient Priest to Modern Physician. Baltimore: Johns Hopkins University Press.

Sheiner LB, Rubin DB (1995).  Intention‐to‐treat analysis and the goals of clinical trials. Clinical Pharmacology & Therapeutics. 57:6-15.

Sinton JA (1926). Studies in Malaria, with special reference to treatment. Part II. The effects of treatment on the prevention of relapse in infections with Plasmodium Falciparum. Indian Journal of Medical Research 13: 579-601.

Stamler J, Pick R, Katz LN (1956). Experiences in assessing estrogen antiatherogenesis in the chick, the rabbit, and man. In: Whitelock OV, Furness FN, Craver BN, eds. (1956). Experimental methods for the evaluation of drugs in various disease states. Annals of the New York Academy of Sciences 64:596-619.

Sutherland I (1958). Statistical aspects of clinical trials. In: Dodds C, ed. Report of a Symposium on Clinical Trials held at The Royal Society of Medicine, London, 25 April, p 53, pp 50-55.

Waife SO, Shapiro AP (1959). The clinical evaluation of new drugs. New York: Hoeber-Harper.

Whitelock OV, Furness FN, Craver BN, eds. (1956). Experimental methods for the evaluation of drugs in various disease states. Annals of the New York Academy of Sciences 64:463-731.

Wiens BL, Zhao W (2007). The role of intention to treat in analysis of noninferiority trials. Clinical Trials 2:286-291.

White IR, Carpenter J, Horton NJ (2012). Including all individuals is not enough: lessons for intention-to-treat analysis. Clinical Trials 9:396-407.

Witts LJ ed. (1959). Medical Surveys and Clinical Trials. London: Oxford University Press.